文献阅读二
Low-Complexity Channel Estimation for Extremely Large-Scale MIMO in Near Field
首先对系统建模
at time instant $l\in{1,\cdots,L}$ ,the received signal at BS can be expressed as
其中
那么对于$L$个snapshot下,M天线的系统模型可以写成
其中$Y$是$M \times L$矩阵,$h$是$M \times 1$向量,就是response vector,s是输入导频数据$1 \times L$
接着先用最小二乘估计h向量,写成优化形式就是极小化$Y-hs$的F范数。
得到结果
h中包含所有的角度距离信息。
有的文章直接用接收信号求信号的协方差来处理,没有用最小二乘处理
这样一般会要求导频数据的协方差$R_S$是单位阵,方便处理。
最小二乘得到h后,便可以信号得到协方差矩阵(二阶统计量)
包含一阶项和二阶项,还是利用对称性来消除二阶项的影响,通过减少原来协方差一个维度的数据来换取解耦。
然后创新点在与解耦以后左右相乘两个DFT矩阵来实现对角度参数的粗估计。
是一个$M_Y \times M_Z$的矩阵
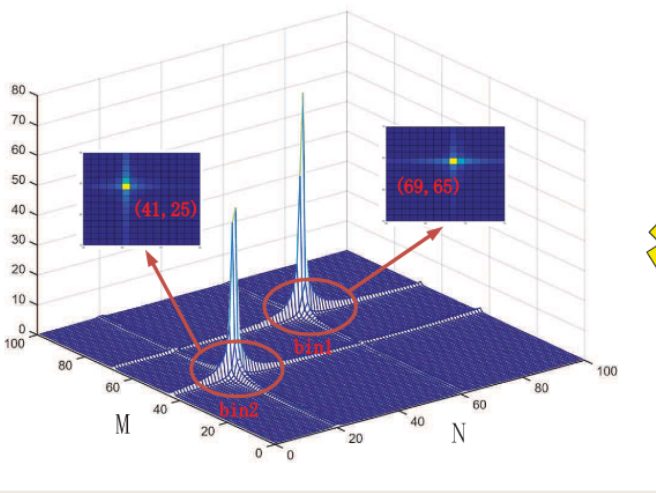
对$e$指数形式的求和必然会出现sin比sin的形式,意思就是只有sin里面等于0才能取到最大值,也就是在二维栅格里的最大的峰值对应粗估计的值。
最终得到粗估计的结引用最初提出DFT论文的一张图。
天线数量越多,所估计的越精确,但遍历所需要时间也越多。
由于天线数量不是足够多的,需要进一步细估计。
大概思路就是:原来由于天线数量不是足够多的,然后使得实际的最高峰一般不能落在整数点上,造成了能量的泄露。那么需要做的就是,移动半个坐标间距,找到最大的值,就是实际距离。
我认为本质上,第一步就是把角度栅格化,去把真实角度落在一个栅格内,这样粗估计用不了多少算力。然后知道最大值就在这个格子内以后,可以移动坐标轴,去把坐标轴对准格子里的最大值,只需要移动半个格子的距离就可以了,这样细估计也用不了多少算力,二维角度估计就快很多。
接着是距离估计,也做了很多细致的优化。
把response vector分成两部分,一部分只与角度有关,另一部分与角度和距离都有关系。
把music转化成了优化问题:
其中
然后求KKT能得到$t$的闭式解,取$t$的相位记为$a$.
由与二次项中距离在分母,误差会很大,相比于直接求music,引入了参数误差项,来减少对结果的影响,又转化成了优化问题:
解法是把$f$构造成了一个矩阵,把$r$和$\sigma$看成了列向量的两个未知数,用最小二乘去解。
DOA estimation exploiting coprime arrays with sparse sensor spacing
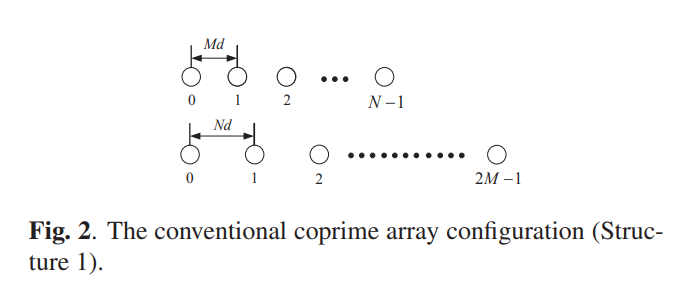
Generalized Coprime Array Configurations for Direction-of-Arrival Estimation
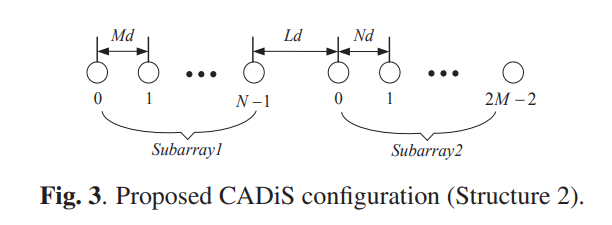
通过在两个子阵之间引入适当的位移,新的互质阵列结构实现了更大的最小元间间距、更多的差集和更大的虚拟阵列孔径。但是连续差集的数量减少了,因为子阵间加了间距后正负差集不再连接。由于空间平滑需要连续差集,所以自由度下降了。