Near-Field Source Localization via Symmetric Subarrays

ESPRIT算法介绍

算法是求远场DOA提出的。
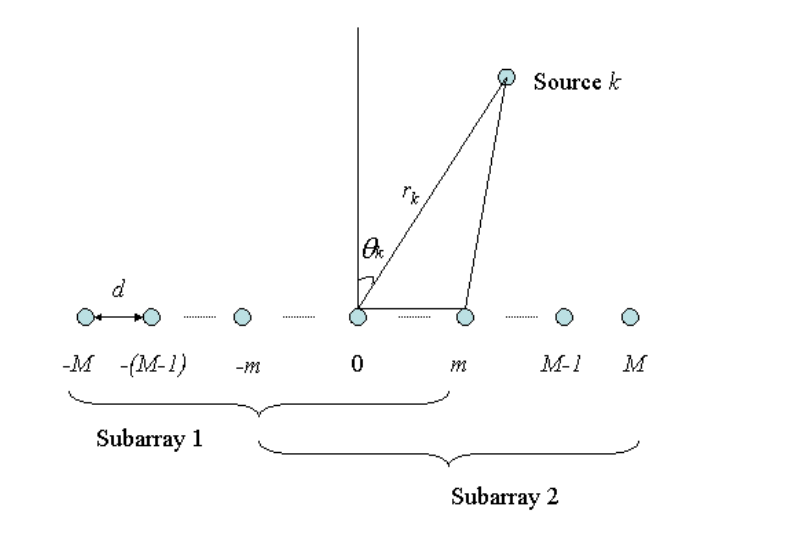
算法假设antennas成对出现，并且两个阵元之间相差已知的位移向量。

这两个subarray response vector分别表示如下：

$\mathbf{x}_{1}=[\mathbf{a}(\theta_{1})\quad\mathbf{a}(\theta_{2})\quad\cdots\quad\mathbf{a}(\theta_{P})]\mathbf{s}+\mathbf{n}_{1}=\mathbf{A}\mathbf{s}+\mathbf{n}_{1}$ $\mathbf{x}_2=\begin{bmatrix}\mathbf{a}(\theta_1)e^{j\phi_1}&\mathbf{a}(\theta_2)e^{j\phi_2}&\cdots& \mathbf{a}(\theta_P)e^{j\phi_P}\end{bmatrix}\mathbf{s}+\mathbf{n}_{2}=\mathbf{A}\mathbf{\Phi}\mathbf{s}+\mathbf{n}_2$

其中steering vector can be expressed as：

$\begin{gathered} \left.\mathbf{a}(r_{k})=\left[\begin{array}{c}{a_{k,-M}}\\{\vdots}\\{a_{k,M}}\end{array}\right.\right]\left.=\left[\begin{array}{c}e^{j\left(\frac{2\pi d}{\lambda}\sin\theta_k\right)M} \\\vdots\\e^{-j\left(\frac{2\pi d}{\lambda}\sin\theta_k\right)M}\end{array}\right.\right]\end{gathered}$

其中${\Phi}$代表旋转算子，是用来将两个子阵联系起来的一个矩阵。

$\Phi = \left.\left[\begin{array}{rrrr}e^{j\phi_1}&&&\\&e^{j\phi_2}&&\\&&\ddots&\\&&&e^{j\phi_p}\end{array}\right.\right]$ $\phi_k=2\pi|\Delta|\sin\theta_k/\lambda$

其中$|\Delta|$是对应两个阵列的间隔，例如图中两个天线阵列的间距为$(M-m)d$。
只要得到两个子阵间的旋转不变关系，就可以得到DOA估计。
将两个子阵的数据合并：

$\mathbf{x}=\begin{bmatrix}\mathbf{x}_1\\\mathbf{x}_2\end{bmatrix}=\begin{bmatrix}\mathbf{A}\\\mathbf{A}\mathbf{\Phi}\end{bmatrix}\mathbf{s}+\begin{bmatrix}\mathbf{n}_1\\\mathbf{n}_2\end{bmatrix}=\bar{\mathbf{A}}\mathbf{s}+\mathbf{n}$

使用数据$\mathbf{x}$来获取协方差矩阵

$R_{xx}=\bar{\mathbf{A}}\mathbf{R_{ss}}\mathbf{\bar{A}}^H+\sigma_n^2\mathbf{I}=\mathbf{E}_s\Lambda\mathbf{E}_s^H+\sigma_n^2\mathbf{E}_n\mathbf{E}_n^H$

信号子空间是由数据矩阵$\mathbf{x}_1$和$\mathbf{x}_2$，也就是矩阵$\bar{\mathbf{A}}$列向量张成的空间。从协方差得到的信号子空间与方向矢量矩阵所张成的空间是一致的。也就是说：

$span(\bar{\mathbf{A}}) = span(E_s)$

因此存在唯一的非奇异满秩矩阵$T$，使得：

$E_s=\bar{\mathbf{A}}T\left.=\left[\begin{matrix}{\mathbf{A}T}\\{\mathbf{A\Phi}T}\\\end{matrix}\right.\right]=\left[\begin{matrix}{E_{s1}}\\{E_{s2}}\\\end{matrix}\right]$

两个子阵的信号空间又有如下关系：

$E_{s2}=E_{s1}T^{-1}\Phi T = {E}_{s1}\mathbf{\Psi}$

我们知道$\Phi$是对角矩阵，且$\Phi$与$\Psi$相似，因此$\Psi$的特征值就是$\Phi$。
在求解中，通过对接收信号分解可以得到信号空间，进而能得到两个子阵信号空间的关系（包括最小二乘法等等来求）,也就是$\Psi$矩阵，之后对其特征值分解可求得$\Phi$。
利用下式即可求得角度：

$\theta_i=\arcsin\left(-\frac{\lambda}{2\pi d}\arg\{z_i\}\right),i=1,\cdots,K$

其中$z_i$是第$i$个特征值。
我认为本质是利用两个子阵信号空间的关系来反映其response vector的关系，进而得到旋转矩阵。

论文insight介绍

对于近场，steering vector可以写成：

$\begin{gathered} \left.\mathbf{a}(r_{k},\theta_{k})=\left[\begin{array}{c}{a_{k,-M}}\\{\vdots}\\{a_{k,M}}\end{array}\right.\right]\left.=\left[\begin{array}{c}e^{j\left(\frac{2\pi d}{\lambda}\sin\theta_k\right)M+j\left(\frac{\pi d^2}{\lambda r_k}\cos^2\theta_k\right)M^2}\\\vdots\\e^{-j\left(\frac{2\pi d}{\lambda}\sin\theta_k\right)M+j\left(\frac{\pi d^2}{\lambda r_k}\cos^2\theta_k\right)M^2}\end{array}\right.\right] \end{gathered}$

我们的想法是提取出旋转矩阵，而且要求旋转矩阵只与角度有关，由于对称项的二阶项系数相等，据此构建旋转矩阵。

$\mathbf{A}=[\mathbf{a}(r_1,\theta_1),\ldots,\mathbf{a}(r_K,\theta_K)]$

两个子阵分别取前L根天线和后L根天线，它们的steering vector可以写成：

$\mathbf{A}=\begin{bmatrix}\mathbf{A}_1\\\text{last}(M-L)\text{rows}\end{bmatrix}=\begin{bmatrix}\text{first}(M-L)\text{rows}\\\mathbf{J}\mathbf{A}_2\end{bmatrix}$

其中$J$矩阵是用来使矩阵反向的。
要消除到二阶项的影响，因此ESPRIT算法中的$|\Delta|$将在两个阵列中不是定值。任意两个对应的天线的$|\Delta|$都会改变。

$\mathbf{A}_2=[\mathbf{D}(\theta_1)\mathbf{a}_1(r_1,\theta_1),\ldots,\mathbf{D}(\theta_K)\mathbf{a}_1(r_K,\theta_K)]$ $\mathbf{D}(\theta_k)=\text{diag}\Big[e^{-j\left(\frac{4\pi d}{\lambda}\mathrm{sin}\theta_k\right)M},\ldots,e^{-j\left(\frac{4\pi d}{\lambda}\mathrm{sin}\theta_k\right)(M-L+1)}\Big]$

同样的，从协方差得到的信号子空间与方向矢量矩阵所张成的空间是一致的。

$E_s={\mathbf{A}}T$ $\left.\mathbf{E}_s=\left[\begin{array}{c}\mathbf{E}_{s1}\\\text{last}(M-L)\text{rows}\end{array}\right.\right]=\left[\begin{array}{c}\text{first}(M-L)\text{rows}\\\mathbf{E}_{s2}\end{array}\right]$

因此可以得到：

$\begin{aligned}\mathbf{E}_{s1}&=\mathbf{A}_1T\\\\\mathbf{E}_{s2}&=\mathbf{J}\mathbf{A}_2T\end{aligned}$

现在问题是无法写出旋转矩阵来描述$A_1$和$A_2$的关系，因为$|\Delta|$和$\theta$都不同。但如果让$\theta$取值都一样是可以写出一个表达关系的，就叫它$A_3$吧。

$\mathbf{A}_3=[\mathbf{D}(\theta)\mathbf{a}_1(r_1,\theta_1),\ldots,\mathbf{D}(\theta_K)\mathbf{a}_1(r_K,\theta)]=\mathbf{D}(\theta)\mathbf{A}_1$

其中当$\theta$对准其中第$i$个用户时候，那个$\mathbf{A}_3$的第i列是与$\mathbf{A}_1$的第$i$列一样的。
那么$\mathbf{A}_3$与$\mathbf{A}_1$两矩阵作差就会得到第$i$列为0，便可以做行列式处理了。

因此可以构造矩阵：

$\mathbf{J}\mathbf{E}_{s2}-D(\theta)\mathbf{E}_{s1}$

这个矩阵也是当$\theta$对准其中第$i$个用户时候，第$i$列为0。
本质还是利用两个子阵信号空间的关系对应其response vector的关系，来求旋转矩阵中的角度。
接着引入任意一个满秩矩阵$W$，求下列表达式谱峰值即可：

$P_{ESPRT}(\theta)=\frac{1}{\det\left[\mathbf{W}^{H}\mathbf{JE}_{s2}-\mathbf{W}^{H}D(\theta)\mathbf{E}_{s1}\right]}$

得到角度估计以后在距离域一维music算法即可。

Mixed Near-Field and Far-Field Source Localization Based on Exact Spatial Propagation Geometry

该文声称：

It is not based on any simplification or approximation on the exact spatial geometry.
The algorithm is applicable to irregularly spaced arrays and can accommodate any arbitrarily and possibly unknown propagation loss.

首先文章定义了四阶累积量如下：

$\begin{aligned} \mathcal{C}(x_{m},x_{n}^{*},x_{p},x_{q}^{*})& =E\{x_{m}x_{n}^{*}x_{p}x_{q}^{*}\}-E\{x_{m}x_{n}^{*}\}E\{x_{p}x_{q}^{*}\}-E\{x_{m}x_{q}^{*}\}E\{x_{p}x_{n}^{*}\}-E\{x_{m}x_{p}\}E\{x_{n}^{*}x_{q}^{*}\} \end{aligned}$

又定义了：

$\boldsymbol{C}_{i}=\mathcal{C}(x_{i}(t),x_{0}^{*}(t),\boldsymbol{x}(t),\boldsymbol{x}^{H}(t)),\mathrm{for~}i=0,1,\ldots,L$ ${C}=[C_{0}^{T},C_{1}^{T},\ldots,C_{L}^{T}]^{T}$

就得到了

$C=\eta(A\odot A)A^H$

接着文中就得到了$A$矩阵？

Source Classification

得到$A$以后那么A的第$\ell$个元素可以写成下列形式：

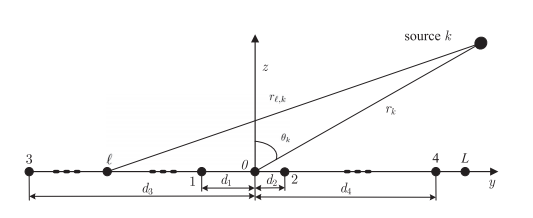
$\hat a_{\ell}(u_{k},r_{k})=\hat b_{\ell,k}^{\frac{p}{2}}e^{j\hat\psi_{\ell,k}}$

那么因为衰减体现在幅度上，信号源的位置信息全体现在相位上。根据两根天线距离$d_1$和$d_2$，可以写出下列方程：

$\begin{cases}r_k-\sqrt{r_k^2+d_1^2-2r_kd_1u_k}=\frac{\hat{\psi}_{1,k}}{2\pi/\lambda}\\r_k-\sqrt{r_k^2+d_2^2-2_kd_2u_k}=\frac{\hat{\psi}_{2,k}}{2\pi/\lambda}\end{cases}$

其中$r_k$和$u_k$分别是第k个源的距离和角度的正弦值。
要求$d_1$和$d_2$是小于半波长的，没有旁瓣，主要做一个粗略估计来区分近场和远场。

Fine Parameter Estimation

同理对$d_3$和$d_4$求解，区别是要求$d_3$和$d_4$大于半波长，这样虽然会出现旁瓣，但是波束宽度窄，可以更精细的估计。旁瓣可以利用粗估计的大致方位来消除。在所有瓣中，选择一个离粗估计最接近的作为细估计的结果。

因此本文认为只需要四个天线的位置即可。

Passive Localization of Mixed Near-Field and Far-Field Sources Using Two-stage MUSIC Algorithm

基于四阶累积量的两阶段MUSIC算法

A Weighted Linear Prediction Method for Near-Field Source Localization

该方法基于均匀线性阵列输出的二阶统计量